











Here is knot 5-1. How is it like 7-1? How is it different?

There are only 2 knots with 5 crossings. 5-1 is one of them. Can you make the other? Does that seem strange to you that there are only 2, when there are 7 different knots with 7 crossings?
Here is knot 9-1.
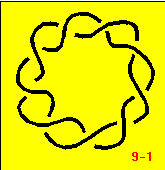
Are you starting to see a family resemblance between 5-1, 7-1, and 9-1? There are forty-nine (!) different knots with 9 crossings. How many of them can you make? Begin by following the patterns that you can see in the 7-crossing knots as they change from 7-1, to 7-2, to 7-3, etc.
Here are knots 6-1 and 8-1. The way they are drawn here, they don't look quite the same as 5-1, 7-1, and 9-1? What makes them different?


Can they be twisted around so that they make nice rings the way 5-1, 7-1, and 9-1 do? What kind of a difference do you think that it might make that 5, 7, and 9 are odd numbers and 6 and 8 are even?