The Ice Cream Stands Problem

Description

Materials

• A copy of the map of Iceberg for each student.
• Overhead transparencies of the Iceberg map and the Secret Solution .

  

Instructions

1. Pass out copies of the map of Iceberg and present the following to the students:

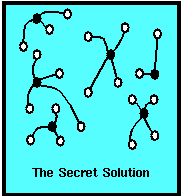
   What you have in your hands is a map of the town of Iceberg. It's a somewhat unusual way to draw a map. The lines on this map represent streets and the dots are street corners. The map doesn't have any houses on it, but we do know that there is at least one house at each corner.

   Iceberg would be a nice place to live, except for one problem: you can't get ice cream anywhere in town. So Ivan and Ivana Icicle have founded the The Icicle & Iceberg Ice Cream Company in order to do something about that. Ivan and Ivana want to do something good for their town, so they are going to build ice cream stands all over town where people can go to buy ice cream. They want it to be easy for the people to get ice cream. They also want to make money.

   At first, Ivan and Ivana had hoped to put an ice cream stand on every corner, knowing how, in the summertime, they would just rake in the money. But ice cream stands are expensive to build: you have to buy all that lumber, and nails, and windows, etc. Then you have to put big freezers inside them, and pay people to work in them all day, and so forth. It didn't seem possible to sell enough ice cream to pay for ice cream stands on every corner.

   They figured, however, that people would still eat lots of ice cream if they only had to walk down the street to get it. Their second plan was to build the ice cream stands so that people could get ice cream either right there on the corner where they live, or at the very most, have to walk down only one street to find a corner where there was an ice cream stand.

   Now, all they have to do is figure out where to put the ice cream stands. Where should they put them? How many do they have to build?

2. Show the students how to use the unifix cubes to mark the places where they think that the ice cream stands should go. Place a marker of one color on a corner where you will put an ice cream stand. Then put markers of a second color on all the corners that are one street away from that ice cream stand. All the people who live in those houses will walk one street to get to the ice cream stand on the next corner.
3. Have the students experiment with their maps and decide where they think the ice cream stands should go. As students find configurations of ice cream stands that will serve all the houses, remind them that the ice cream stands are expensive to build, and that Ivan and Ivana want to build as few as possible. Ask if there's any way to rearrange their configuration of ice creams stands so that one or more can be eliminated.
4. You can tell students that it is possible to build only 6 ice creams stands and serve all of the houses in this town, or you can let them try to discover that this is the minimum on their own.
5. After students have had a chance to work on the puzzle and solve it, show them how it was made.
   • Display the transparency of the Secret solution .
   • Explain that you can make a puzzle like the Ice Cream Stands Puzzle by drawing the solution first. It is easy to see what the solution to the puzzle is when looking at the Secret Solution .
   • Then lay the map of Iceberg over the Secret Solution on the overhead. Almost by magic, the easy-to-see solution disappears. After drawing the solution to the puzzle, the puzzle-maker draws just enough disguising lines to make the solution hard to find.
   • Invite students to make a similar puzzle of their own.
   • It is not necessary to make puzzles with ice cream stands only. Perhaps the students would like to make a puzzle about something that is more interesting to them than ice cream. One way to begin is by asking, "What kinds of things do you think a town should have many of so that there is one close to everyone's house?" Students' ideas may include: convenience stores, video rentals, swimming pools, shopping malls, parks etc.

Discussion

1. What strategies did you use to try to figure out where to put the ice cream stands? How did you check to make sure that no house was too far away from an ice cream stand? Do you think it is possible to arrange the ice cream stands in a different way so that Ivan and Ivana won't need to build so many of them?
2. How did you make your own puzzle? If you didn't use ice cream stands in the puzzle that you made, how did you decide what to use instead? What happened when you showed your puzzle to other people? Were they able to solve it?
3. Do you think it would be possible to make a puzzle like this, and then come up with a solution that is even better (i.e., takes fewer ice cream stands) than the one you built into the puzzle in the first place? Try to make a puzzle where that happens.
4. Explain to students that this puzzle is an example of what mathematicians call a one-way function . If you start with the solution and create the puzzle it's easy. If you start with the puzzle and have to find the solution it's not. One way it's easy, one way it's hard. A place that one-way functions are useful is for inventing secret codes. When you have a good scheme for a secret code, it is easy to encode a secret message, but difficult to decode it. Invite students to find other examples of one-way functions.
5. Ask students to think of other situations in real life that might present themselves as a puzzle like this. Some of their ideas might include: finding locations for warehouses, main and branch offices, electrical switching stations, telecommunication centers, airports, hamburger joints, hospitals, firestations, and restrooms. Remind students that when people are faced with problems like this in real life, someone hasn't made the puzzle ahead of time. Trying to find strategies for solving puzzles like this is important when you can't just say, "I give up. What's the solution?"

What next?