
You can't count to infinity. Yet we are comfortable with the idea that there are infinitely many numbers to count with: no matter how big a number you might come up with, someone else can come up with a bigger one: that number plus one--or plus two, or times two. Or times itself. There simply is no biggest number. Is there?
Is infinity a number? Is there anything bigger than infinity? How about infinity plus one? What's infinity plus infinity? What about infinity times infinity? Children to whom the concept of infinity is brand new, pose questions like this and don't usually get very satisfactory answers. For adults, these questions don't seem to have very much bearing on daily life, so their unsatisfactory answers don't seem to be a matter of concern.
At the turn of the century, in Germany, the Russian-born mathematician Georg Cantor applied the tools of mathematical rigor and logical deduction to questions about infinity in search of satisfactory answers. His conclusions are paradoxical to our everyday experience, yet they are mathematically sound. The world of our everyday experience is finite. We can't exactly say where the boundary line is, but beyond the finite, in the realm of the transfinite, things are different.
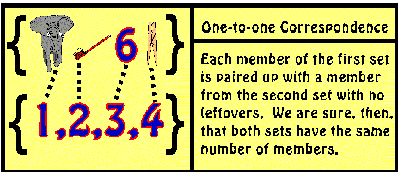
The set is the mathematical object which Cantor scrutinized. He defined a set as any collection of well-distinguished and well-defined objects considered as a single whole. A collection of matching dishes is a set, as well as a collection of numbers. Even a collection of seemingly unrelated things like, {toothbrush, elephant, clothespin, 6} is a set. They are well-defined and can be distinguished from one another.

Sets can be large and small. They can also be finite and infinite. A finite set has a finite number of members. No matter how many there are, given enough time, you can count them all. Cantor's surprising results came when he considered sets that had an infinite number of members. Sets such as all of the counting numbers, or all of the even numbers are infinite sets.
In order to study infinite sets, Cantor first formalized many of the things that are intuitive and obvious about finite sets. At first, it seems like these formalizations are just a whole lot of trouble, a way of making simple things complicated. Because the formalisms are clearly correct, however, they provide a powerful tool for examining things that are not so simple, intuitive or obvious.
You can't count the members in an infinite set, though, so this method won't work for comparing their sizes. If you have two infinite sets, you need some other way to tell if one is larger.
The formal notion that Cantor used for comparing sizes of sets is the idea of a one-to-one correspondence. A one-to-one correspondence pairs up the members of one set with the members of another. We could pair up the elements of the ridiculous set {toothbrush, elephant, clothespin, 6} with the numbers {1,2,3,4}. It is possible to do this so that one member of each set is paired up with one member of the other, no member is left out, and no member has more than one partner. Then we can be sure that the set {1,2,3,4} has the same number of members as the set {toothbrush, elephant, clothespin, 6}

Our intuition tells us that the set with the shoe in it must be bigger. Can we be sure? The set of counting numbers has an infinite number of members. How can the set with the shoe in it have more than an infinite number of members?
The set of all counting numbers is {1,2,3,... }. Is there a way to put its members in a one-to-one correspondence with the set {shoe, 1, 2, 3}? If they come out even, then we can be sure the two sets are the same size. If one set has members left over when the other set has used up all of its members, then we will know which set is bigger. The answer (believe it or not) is that yes! the two sets can be put in one-to-one correspondence with each other, and yes! they are the same size.

Our intuition and experience with finite things in the world makes us want to protest that when we pair up the members of these sets, the set without the shoe, will run out of members before the other one does. But these are infinite sets. We will not get to the end. Neither set will run out of members. The pairing goes on and on. Ad infinitum.
In The Hotel Infinity the pairing of hotel guests with hotel rooms puts the members of a set of hotel guests in one-to-one correspondence with a set of hotel rooms.
Infinity plus one is infinity. Once you slip into the realm of the infinite, the rules of arithmetic are not the same anymore. The rules of transfinite arithmetic take over.

We won't run out of even numbers before we run out of counting numbers or vice versa, so the members of the two sets can be placed in one-to-one correspondence with each other. This means that they are the same size. There are as many even numbers as there are counting numbers. Infinity times two is infinity. Infinity divided by two is infinity. These are the kinds of conclusions which caused Georg Cantor to say, "I see it, but I do not believe it."
Part of the set of rational numbers consists of {1/1, 1/2, 1/3, 1/4,...}. These are all the fractions whose numerator is one. There are an infinite number of those. Then there are {2/1, 2/2, 2/3, 2/4...} These are all the fractions whose numerators are 2--another infinite set. We could make infinitely many such lists, each one with infinitely many rational numbers on it. So to figure out how many rational numbers there are, all we would have to do would be multiply infinity times infinity. Certainly that must be more than infinity.
We can't just say that it seems like there are more rational numbers than counting numbers, we have to prove that there are. If we want to say that infinity times infinity is bigger than infinity, then we have to show how the set with infinity-times-infinity members (the rational numbers) cannot be put into a one-to-one correspondence with the set that has an infinite number of members (the counting numbers).
When the all of the busses pulled up to the Hotel Infinity, fully loaded, with everyone on them needing a room, it was as though all of the rational numbers showed up to a dance where all of the counting numbers were, and everyone started looking for a partner. If you imagine each person on the bus as having a bus number and a seat number, you can list the people on the first bus as {1/1, 1/2, 1/3,...} the people on the second bus would be listed as {2/1, 2/2, 2/3...} in the story, George had an idea for finding a room for every person on the busses. If his idea works, you can pair up every rational number with a counting number. Could it be true that infinity times infinity is infinity?
Some mathematicians who lived at the end of the 19th century (the same time as Cantor lived) did not want to accept his work at all. The fact that his results were so paradoxical was not the problem so much as the fact that he considered infinite sets at all. At that time, some mathematicians held that mathematics could only consider objects that could be constructed directly from the counting numbers. You can't list all the elements in an infinite set, they said, so anything that you say about infinite sets is not mathematics. The most powerful of these mathematicians was Leopold Kronecker who even developed a theory of numbers that did not include any negative numbers.
Although Kronecker did not persuade very many of his contemporaries to abandon all conclusions that relied on the existence of negative numbers, Cantor's work was so revolutionary that Kronecker's argument that it "went too far" seemed plausible. Kronecker was a member of the editorial boards of the important mathematical journals of his day, and he used his influence to prevent much of Cantor's work from being published in his lifetime. Cantor did not know at the time of his death, that not only would his ideas prevail, but that they would shape the course of 20th century mathematics.