In mathematics we are concerned with mathematical truth (and falsity) based on proof that use the rules of logic. (See also True, False, and the Mathematician's Logic.)
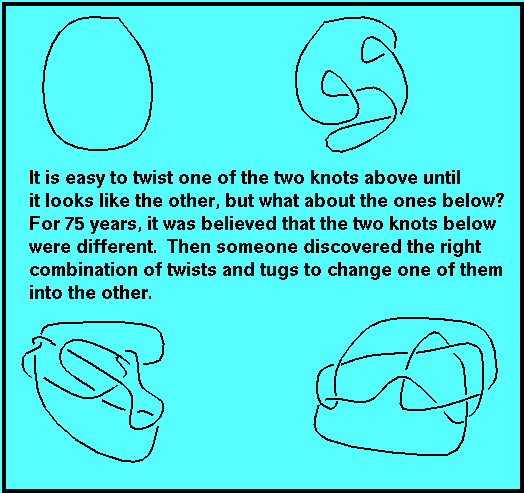
No statement or assertion can be taken as true unless it has been rigorously demonstrated using logic. Even the most plausible, believable, and well-accepted notions remain conjectures until they are proved. A statement can seem true, and for many years people try and cannot find and reason for it to be false. Such a statement does not become a theorem in mathematics until it has been proved.

Sometimes this results in a complex relationship between mathematical knowledge and knowledge gained from intuition, guessing, and experience in the world. For instance, pursuing a notion with mathematical rigor can lead to contradictions or paradox. (See Infinity is for Children and Mathematicians!)


