The mathematical theory of knots has made major advances in the past decade. One of the most exciting developments has been the discovery of deep connections between knot theory and the branch of physics that studies the fundamental particles and forces that are the building blocks of the universe. It has also been found that DNA is sometimes knotted, and knots may play a role in molecular biology.
Mathematicians envision knots as closed loops or paths that you can trace round and round with your finger. It is as though the two free ends of tangled rope have been spliced together. When knots are drawn or represented on paper, the places where the rope crosses itself are shown as a broken line and a solid line. The intent is to show that the part of the rope represented by the broken line is passing under the part represented by the solid line.
A knot is a mathematical object , just like number is, and mathematicians ask many of the same questions about knots as they have asked about numbers. One of these questions is, "Are these two knots equal?"

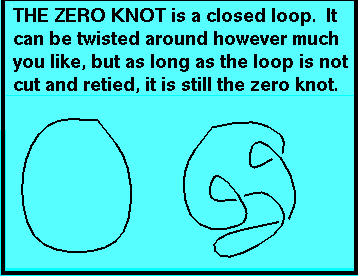
Notice how the knot on the right in the picture above can be untangled, without cutting, to look like the knot on the left. This is the concept of knot equivalence. When two knots seem to be very different, it could very well be that one is just an extra-twisted-up verstion of the other, and that one knot can be transformed into the other by twisting and turning, but without cutting the rope and actually unknotting it.
But on the other hand, when two knots, such as the trefoil knots below seem similar at a glance, this is not always the case.

Knot theorists are still seeking a straightforward and general method for determining whether two knots are equivalent. When students try to determine what it is about two knots that make them the same, even though they may be twisted about so that their forms appear different, they are grappling with the concept of topological equivalence. This notion is a very powerful idea that plays many roles throughout mathematics.
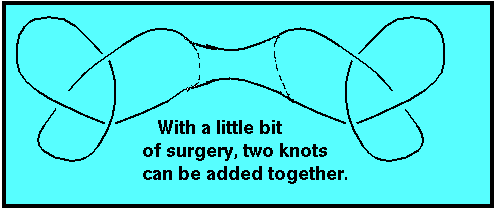
What is knot addition and how does it work? You can "add" two knots together if you make a cut in each one, and, without unknotting, splice the ends together so that each end is joined to an end from the other knot. An example of knot addition is shown in the picture. The Zero Knot is so named, not just because it makes the shape of an "O", but also because it behaves like the number zero. When you add the Zero Knot to another knot, there is a little bit more rope, but the knot itself is unchanged.
What are the basic knot building blocks? Knot addition shows us how two knots can be added together to make a more complex knot. How does this work in reverse? Can you always break a complicated knot into two simpler ones that add together to form it? Of course the answer to that question implies that we know what complex and simple knots are!
This question is analogous to thinking about prime numbers (2, 3, 5, 7, 11, etc.).
You cannot find two counting numbers that you can multiply together to give you a prime number (except the prime number and 1, of course). All numbers that are not prime can be produced by multiplying together a unique combination of prime numbers. Is the same thing true with knots? Indeed, there are prime knots--very many of them--that exist for knot addition. Determining whether a knot is made of smaller building blocks is not always very easy, but it is interesting and challenging to try.
Are there negative knots? When we add the negative number -2 to the number 2 the result is 0. Are there pairs of knots that you can add together and end up with the Zero Knot?

Can knots double up? What do you get, for example, if you begin with a knot, then take a second piece of rope and make a knot out of it that is woven into the first knot? The result is what mathematicians call a link. Links can be made up of any number of connected knots, and we can ask all the same questions about links as we can about knots--and then we can invent some more. Perhaps this gives you some idea why, although the idea of a knot is very simple, mathematically, the territory is enormously vast.

Where do braids fit in? If you take a braid that is made of three or four, or any number of strands, you can splice the ends in a variety of ways. You can turn it into a knot, or you can turn it into a link made of several intertwined knots. As usual, questions abound, and the potential for discoveries is great.
Seeking information about knots by experimenting with them and reasoning about them leads to some observations about mathematical proof and the idea of mathematical truth .
For example, when we defined knot equivalence, we said that two knots were equivalent when one can be transformed into the other without cutting and unknotting. With a little bit of experimentation, we can demonstrate how to do this for the top two knots in the picture below. We could even write up a set of instructions so that someone else could do it, too.
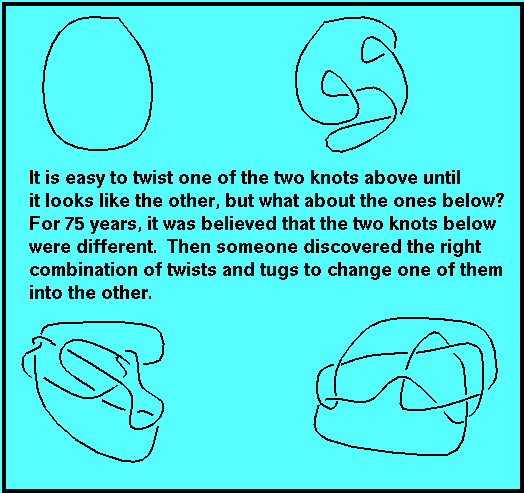
For two knots that are very complex, we can try a long time to rearrange them so that they look alike and not succeed. How long is long enough? It took 75 years before someone showed that the bottom two knots in the picture above were equivalent.
In mathematics, you can prove that something can be done by demonstrating how to do it. You cannot prove that something cannot be done by saying, "I tried and tried for a very long time. I tried very hard, but I couldn't do it." Often, it is very tricky to prove mathematically that something can't be done.
Here are some stragegies that sometimes work if you want to prove that something is impossible to do:
When children explore knot theory they will be able to demonstrate, after varying amounts of puzzling and experimentation, that various knots are equivalent, that certain knots can be decomposed into simpler forms, and so forth. They will invent questions of their own and perhaps answer them. In certain cases they will undoubtedly be surprised to discover that things which they thought were impossible could be done after all.
At first, students might be uncomfortable and frustrated with the experience of having open questions and unsolved problems mount up faster than closed issues and clear answers. This, however, has always been the situation in mathematics (and science generally). Although discoveries, solutions, and answers abound, they are rare in relation to the number of things that are not known. This is why discovering something new or solving a problem is a reason to be pleased and excited.